אות שמע – אותות מחזוריים
אות מחזורי (Periodic Signal) הוא אות אשר כל מחזור בו מהווה העתק מדויק של קודמו.
רכיביו של אות מחזורי הינם מסוימים, ז”א תמונתו הספקטראלית אינה משתנה עם הזמן.
האינפורמציה שבאות מחזורי משתקפת כולה בתמונתו הספקטראלית, ז”א במשטר התדר.
משטר הזמן לא מעניק כל מידע נוסף אודות האות.
תדירותו של אות מחזורי היא לכל היותר כזו של רכיבו הנמוך ביותר.
האות המחזורי הפשוט ביותר הוא סינוסואידה מתמשכת. לאות זה רכיב (תדר) יחיד בעל משרעת קבועה, וניתן להפיקו באמצעות גנרטור (מחולל אותות).
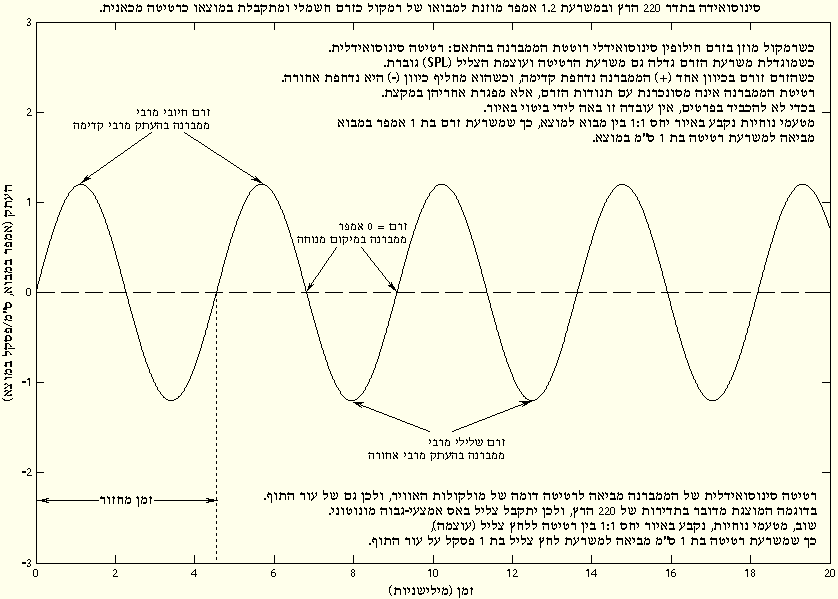
אם נזין סינוסואידה כזו למבואו של רמקול (כזרם חשמלי), תרטוט הממברנה בהתאם: רטיטות גליות “חלקות” שקצבן זהה לתדירות הסינוסואידה ומשרעתן מתאימה למשרעתה.
בהתאם ירטוט גם האוויר.
אם תדירות הסינוסואידה תהיה בתחום 20-20,000 הרץ יתקבל אות שמע.
כדי שנוכל לשומעו על משרעת הרטיטות להיות גבוהה מספיק, כך שעל עור התוף יופעל לחץ צליל (SPL) גבוה מסף השמע.
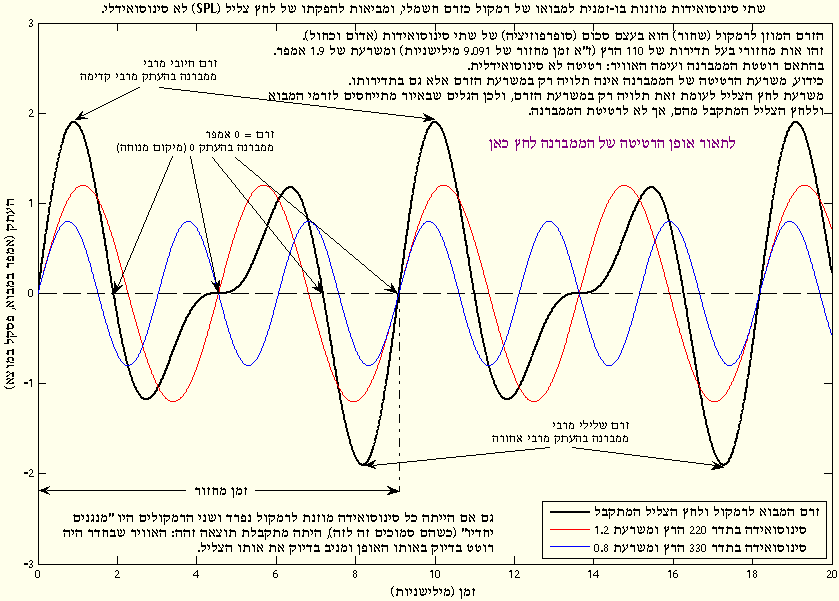
אות מחזורי מורכב יותר מתקבל ממיזוגן של שתי סינוסואידות כנ”ל המופקות בו זמנית, כ”א בתדר אחר.
משרעותיהן יכולות להיות שונות זו מזו או זהות זו לזו.
לאות שכזה שני רכיבים (תדרים) בעלי משרעת קבועה, ותדירותו היא לכל היותר כזו של הרכיב הנמוך.
אם נזין אות זה למבואו של רמקול (כזרם חשמלי) תרטוט הממברנה בהתאם: רטיטות לא “חלקות” שקצבן זהה לתדר האות.
צורת הרטיטה תושפע בעיקר מהרכיב הנמוך, כיוון שמשרעת הרטיטה גדולה יותר בתדרים נמוכים.
עם זאת, יחסי העוצמה האקוסטיים שבין הרכיבים יישמרו כפי שהיו בגרסתו החשמלית של האות.
באופן מפתיע, אם תוזן כל סינוסואידה בנפרד לרמקול “משלה” ושני הרמקולים ימוקמו בסמיכות ו”ינגנו יחדיו”, ירטוט האוויר בדיוק כפי שרטט קודם.
תופעה זו נובעת מ”עקרון ההתאבכות” (“סופרפוזיציה”), אשר תקף לכל תהליך ליניארי:
אין זה משנה אם הסינוסואידות מוזגו כאותות חשמליים והוזנו לרמקול יחיד, או אם הוזנו בנפרד לרמקולים נפרדים ומוזגו רק אח”כ כגלי קול סינוסואידליים.
האפשרות השנייה פשוט יקרה יותר, כיוון שנחוץ אז יותר מרמקול אחד.
אות מחזורי מורכב עוד יותר הוא האות המתקבל מכלי נגינה שמנגן תו יחיד באופן מתמשך ויציב.
במקרה זה קיים קשר הרמוני בין רכיבי האות, ז”א תדירותו של
כל רכיב מהווה כפולה שלמה של תדירות הרכיב הנמוך ביותר.
הרכיב הנמוך ביותר מכונה אז “פנדמנטאל”, ושאר הרכיבים מכונים “הרמוניות”.
לדוגמה, כלי המנגן את התו A3 מפיק פנדמנטאל בתדר 220 הרץ, הרמוניה שנייה בתדר 440 הרץ, הרמוניה שלישית בתדר 660 הרץ וכן הלאה.
כך הוא בכל כלי נגינה המנגן את התו A3, יהא זה טרומבון, כינור או כל כלי אחר.
כולם יציגו תמונה ספקטראלית המכילה את אותן ההרמוניות.
מדוע אם כן נשמע הטרומבון שונה מהכינור, אפילו כששניהם מנגנים את התו A3?
בשל יחסי העוצמה השונים שבין ההרמוניות.
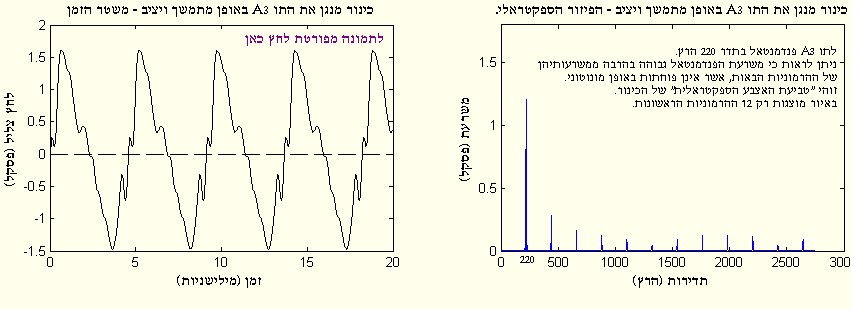
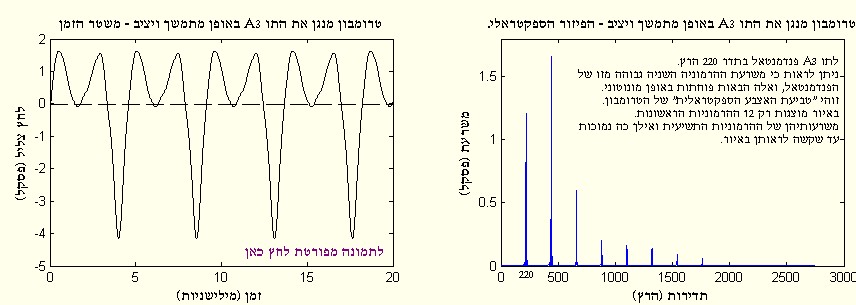
בתרשים הבא ניתן לראות כי לכינור פנדמנטאל דומיננטי, לעומת הטרומבון בו דומיננטית ההרמוניה השנייה.
ברוב הכלים דומיננטי הפנדמנטאל, כך שהטרומבון הינו יוצא דופן מבחינה זו.
חליל הצד הינו דוגמה לקיצוניות הפוכה: פנדמנטאל עתיר אנרגיה עם נוכחות מועטה מאוד של הרמוניות.
לכן, מכל הכלים, חליל הצד מפיק את האות הדומה ביותר לסינוסואידה.
כל כלי נגינה מאופיין אם כן ביחס עוצמות מסוים בין ההרמוניות, היחס ההרמונאלי, אשר גורם לו להישמע כפי שהוא נשמע.
לכלים מאותו סוג יש יחס הרמונאלי כה דומה, עד שרק מומחה מסוגל להבדיל בין שני פרטים שונים, שני כינורות למשל.
ומה לגבי מופען של ההרמוניות, או ליתר דיוק, הפרשי המופע שבין ההרמוניות?
ובכן, לכל כלי ישנם הפרשי מופע אופייניים בין ההרמוניות, אשר ביחד עם היחס ההרמונאלי יוצרים את צורת האות האופיינית לו.
מסקרן לדעת אם שני אותות בעלי יחס הרמונאלי זהה אך הפרשי מופע שונים בין ההרמוניות נשמעים שונים זה מזה, והתשובה היא – בד”כ לא.
בעלי סינתיסייזר או תוכנת מחשב מתאימה יכולים לבדוק זאת בעצמם, כל שעליהם לעשות הוא להפיק סינוסואידה אשר תשמש פנדמנטאל לתו כלשהו (למשל בתדר 440 הרץ המהווה פנדמנטאל לתו A4), ובו זמנית להפיק סינוסואידות בתדרים הרמוניים מתאימים (עבור A4 בתדרים 880 הרץ, 1320 הרץ וכן הלאה).
בעזרת שינוי עוצמתן היחסית של הסינוסואידות ניתן לשנות לחלוטין את הצליל המתקבל, כך שפעם יישמע דומה לכינור, פעם לטרומבון ופעם לכלי שאינו קיים בכלל.
לעומת זאת שינוי הפרשי המופע שבין הסינוסואידות ספק אם ישפיע על אופי הצליל המתקבל – אוזננו אדישה בד”כ להפרשי מופע כשמדובר באות מחזורי.
כדאי לשים לב לכך שצורת האות משתנה באופן דרמטי כתוצאה משינוי הפרשי המופע, ז”א יתכנו אותות בעלי צורה שונה לחלוטין אשר נשמעים זהים זה לזה.
עם זאת ישנם אותות מחזוריים מסוימים אשר בהם שינוי הפרשי המופע יכול להיות שמיע.
אותות אלה מאופיינים לרוב בנוכחות בולטת של הרמוניות זוגיות ובא-סימטריה קיצונית, ז”א החלק החיובי שלהם שונה מאוד בצורתו ובמשרעתו מהחלק השלילי.
שינוי הפרשי המופע עלול לטשטש את אי הסימטריות שלהם, ואוזננו שניחנה בקורטוב של אי-ליניאריות א-סימטרית מסוגלת להבחין בכך לעיתים.
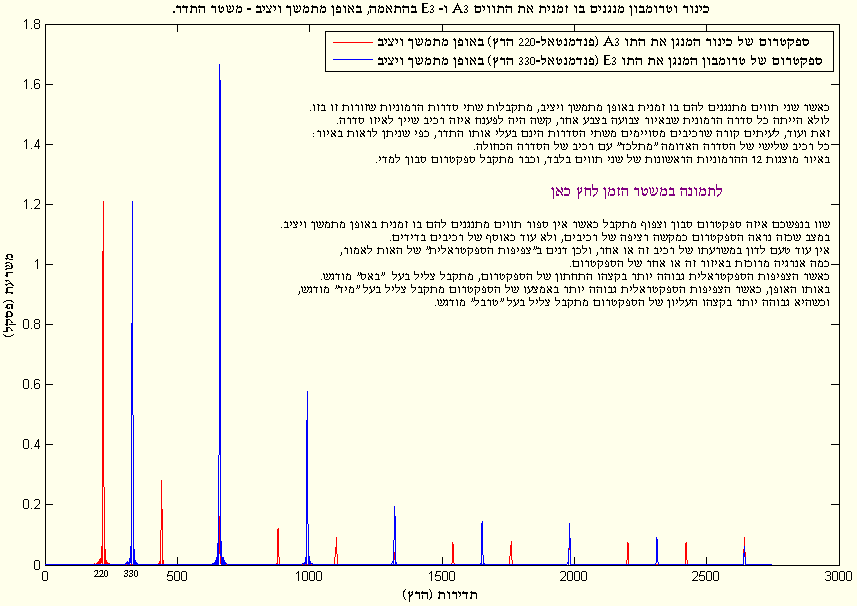
אם ינגן הכלי שני תווים בו זמנית (אקורד) באופן מתמשך ויציב, A3 ו- E3 למשל, יתקבל אות מחזורי מורכב עוד יותר.
כעת לא יהיה עוד קשר הרמוני בין רכיבי האות.
כ”א משני התווים יפיק אומנם סדרת רכיבים הרמונית, אך הסדרה שתתקבל משתי הסדרות כשהן שלובות יחדיו לא תהיה הרמונית.
מספר הרכיבים מהם בנוי האות יגדל, וקצת קשה יהיה לזהות לאיזו משתי הסדרות ההרמוניות שייך רכיב זה או אחר.
בתרשים שלהלן מנוגן כל תו ע”י כלי אחר, כדי לעשותה יותר מעניינת.
ע”פ אותו העיקרון, אם ינגן הכלי אקורד בן שלושה תווים, E3, A3, ו-C3 למשל, יגדל עוד יותר מספר הרכיבים מהם בנוי האות, וכך הלאה בהתאם למספר התווים המרכיבים את האקורד.
שילובן יחד של מספר סדרות הרמוניות מקטין את הסיכוי למצוא רכיבים סמוכים השייכים לאותה סדרה הרמונית, ז”א לאותו תו.
נוצר לכן הרושם כי רכיבי האות מפוזרים לרוחב הספקטרום באופן אקראי.
ניתן לדבר בהקשר זה על צפיפותו הספקטראלית של האות לאמור, כמה מרכיביו ממוקמים באזור זה או אחר של הספקטרום.
על אזור בו ממוקמים רכיבים רבים יותר נאמר כי הוא צפוף יותר מבחינה ספקטראלית.
בד”כ תרוכז באזור שכזה גם מרבית האנרגיה שבאות, אך לא בהכרח.
יתכן כי באזור אחר שהינו פחות צפוף ממוקמים רכיבים בעלי משרעת גבוהה יותר אשר “יכריעו את הכף לטובתו” מבחינה אנרגטית.
ככל שמרוכזת יותר אנרגיה באזור הנמוך של הספקטרום, מתקבל צליל יותר “באסי”.
באותו אופן, ככל שמרוכזת יותר אנרגיה באזור הגבוה של הספקטרום מתקבל צליל יותר “טרבלי”.
כעת שוו בנפשכם אקורדיון אשר בין מנענעו הנמוך ביותר לזה הגבוה ביותר “דחפו” הרבה יותר מנענעים מהמקובל.
אקורדיון שכזה יפיק לא רק תווים “מקובלים” (C, B, A וכן הלאה) אלא גם אין ספור תווים שבניהם.
כל המנענעים נלחצים יחדיו, כך שכל התווים הרבים והשונים מתנגנים בו זמנית באופן מתמשך ויציב.
כל תו מפיק סדרת רכיבים הרמונית, אך שילובן של כל הסדרות יחדיו נראה כאוסף עצום ואקראי של רכיבים המצטופפים לרוחב הספקטרום.
לו היה מספר המנענעים אינסופי היה בהתאם גם מספר התווים אינסופי ולכן, על אחת כמה וכמה, גם מספר הרכיבים המצטופפים לרוחב הספקטרום.
במצב תיאורטי זה תהיה צפיפות הרכיבים אינסופית, ולכן תתקבל תמונה רציפה של צפיפות ספקטראלית במקום זו הבדידה שהתקבלה קודם לכן.
כעת לא יהיה עוד טעם לדבר על רכיבים אלה או אחרים המרכיבים את האות, כיוון שממילא הוא יהיה מורכב מכל הרכיבים (תדרי השמע) שישנם בעולם.
המושג “צפיפות ספקטראלית” אשר קודם לכן התייחס לצפיפות הרכיבים באזור זה או אחר של הספקטרום, יתייחס כעת לכמות האנרגיה הנמצאת באזור הנדון.